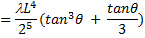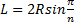The Moment of Inertia of a Regular Polygon
The Polygon can be divided into n congruent triangles. Let
us find the Moment of Inertia of one such triangle about the polygon’s center.
And since Moment of Inertia is a scalar quantity, multiplying
it by n, will give us the Moment of Inertia of the entire polygon.
 |
The triangle can be imagined to be made up of infinite
number of rods. Let us take such a rod, of length 2x(figure), and width dy.
Let the Mass per unit area of the polygon (or, the triangle)
be λ.
Area of rod = 2.x.dy
Mass of rod = λ.2.x.dy
By the parallel axis theorem,
Moment of Inertia of the rod about O = Moment of
Inertia of rod about C + m.OC2.
Where C is the Center of Mass of the rod and m is the mass
of the rod (=2λ.x.dy).
Therefore,
Which gives,
Now, since
We have
Let the total mass of the polygon = M
Therefore
Therefore,
Further,
Therefore,
Multiplying the above value of I
by
n, we have the Moment of Inertia for the entire polygon
Here L represents the length of one side of the polygon.
If the circum-radius R of the polygon is given, then putting
We have
Clearly for a circular disc we have n→ ∞,
the value of I becomes